Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 05, pp. 1-12.
Stability of peakons for the generalized Camassa-Holm equation
Orlando Lopes
Abstract:
We study the existence of minimizers for a constrained variational
problems in
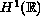 .
These minimizers are stable
waves solutions for the Generalized Camassa-Holm equation,
and their derivative may have a singularity
(in which case the travelling wave is called a peakon).
The existence result is based on a method developed by the same
author in a previous work. By giving examples, we show how
our method works.
.
These minimizers are stable
waves solutions for the Generalized Camassa-Holm equation,
and their derivative may have a singularity
(in which case the travelling wave is called a peakon).
The existence result is based on a method developed by the same
author in a previous work. By giving examples, we show how
our method works.
Submitted October 25, 2002. Published January 7, 2003.
Math Subject Classifications: 35J20, 49J10.
Key Words: variational problems, stability of peakons.
Show me the
PDF file (248K),
TEX file for this article.
Orlando Lopes
Departamento de Matematica-IMECC-UNICAMP-
C.P. 6065 Campinas, SP 13083-859, Brasil
e-mail: lopes@ime.unicamp.br
Return to the EJDE web page
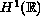 .
These minimizers are stable
waves solutions for the Generalized Camassa-Holm equation,
and their derivative may have a singularity
(in which case the travelling wave is called a peakon).
The existence result is based on a method developed by the same
author in a previous work. By giving examples, we show how
our method works.
.
These minimizers are stable
waves solutions for the Generalized Camassa-Holm equation,
and their derivative may have a singularity
(in which case the travelling wave is called a peakon).
The existence result is based on a method developed by the same
author in a previous work. By giving examples, we show how
our method works.