This work presents new results about the instability of solitary-wave solutions to a generalized fifth-order Korteweg-deVries equation of the form
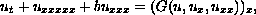
where
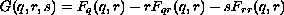 for some
for some
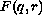 which is homogeneous of degree
which is homogeneous of degree
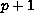 for some
for some
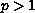 .
This
model arises, for example, in the mathematical description of
phenomena in water waves and magneto-sound propagation in plasma.
The existence of a class of solitary-wave solutions is obtained by
solving a constrained minimization problem in
.
This
model arises, for example, in the mathematical description of
phenomena in water waves and magneto-sound propagation in plasma.
The existence of a class of solitary-wave solutions is obtained by
solving a constrained minimization problem in
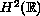 which
is based in results obtained by Levandosky. The instability of
this class of solitary-wave solutions is determined for
which
is based in results obtained by Levandosky. The instability of
this class of solitary-wave solutions is determined for
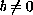 ,
and it is obtained by making use of the variational
characterization of the solitary waves and a modification of the
theories of instability established by Shatah & Strauss,
Bona & Souganidis & Strauss and Goncalves Ribeiro. Moreover,
our approach shows that the trajectories used to exhibit instability
will be uniformly bounded in
,
and it is obtained by making use of the variational
characterization of the solitary waves and a modification of the
theories of instability established by Shatah & Strauss,
Bona & Souganidis & Strauss and Goncalves Ribeiro. Moreover,
our approach shows that the trajectories used to exhibit instability
will be uniformly bounded in
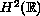 .
.
