Electron. J. Diff. Eqns., Vol. 2003(2003), No. 102, pp. 1-7.

Periodic solutions for neutral nonlinear differential equations with functional delay

Youssef N. Raffoul

Abstract:
We use Krasnoselskii's fixed point theorem to show that the nonlinear neutral differential equation with functional delay
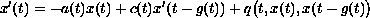
$$ x'(t) = -a(t)x(t)+ c(t)x'(t-g(t))+ q\big(t, x(t), x(t-g(t)\big) $$
has a periodic solution. Also, by transforming the problem to an integral equation we are able, using the contraction mapping principle, to show that the periodic solution is unique.

Submitted April 22, 2003. Published October 6, 2003.
Math Subject Classifications: 34K20, 45J05, 45D05.
Key Words: Krasnoselskii, neutral, nonlinear, integral equation, periodic solution, unique solution.

Show me the PDF file (181K), TEX file, and other files for this article.

Youssef N. Raffoul
Department of Mathematics
University of Dayton
Dayton, OH 45469-2316 USA
e-mail: youssef.raffoul@notes.udayton.edu

Return to the EJDE web page