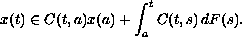This paper studies the functional differential equation
![$$
\dot x(t) = \int_a^t {d_s R(t,s)\, x(s)} + F'(t), \quad t \in [a,b],
$$](gifs/aa.gif)
where
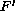 is a generalized derivative, and
is a generalized derivative, and
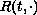 and
and
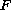 are functions of bounded variation.
A solution is defined by the difference
are functions of bounded variation.
A solution is defined by the difference
 being absolutely continuous and satisfying the inclusion
being absolutely continuous and satisfying the inclusion
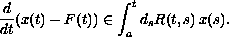
Here, the integral in the right is the multivalued Stieltjes integral presented in [11] (in this article we review and extend the results in [11]). We show that the solution set for the initial-value problem is nonempty, compact, and convex. A solution
 is said to have memory if there exists the function
is said to have memory if there exists the function
 such that
such that
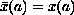 ,
,
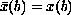 ,
,
![$\bar x(t) \in [x(t-0),x(t+0)]$](gifs/ak.gif) for
for
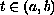 , and
, and
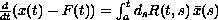 ,
where Lebesgue-Stieltjes integral is used.
We show that such solutions form a nonempty, compact, and convex
set. It is shown that solutions with memory obey the Cauchy-type
formula
,
where Lebesgue-Stieltjes integral is used.
We show that such solutions form a nonempty, compact, and convex
set. It is shown that solutions with memory obey the Cauchy-type
formula