We start by introducing a new definition of solutions to heat-based SPDEs driven by space-time white noise: SDDEs (stochastic differential-difference equations) limits solutions. In contrast to the standard direct definition of SPDEs solutions; this new notion, which builds on and refines our SDDEs approach to SPDEs from earlier work, is entirely based on the approximating SDDEs. It is applicable to, and gives a multiscale view of, a variety of SPDEs. We extend this approach in related work to other heat-based SPDEs (Burgers, Allen-Cahn, and others) and to the difficult case of SPDEs with multi-dimensional spacial variable. We focus here on one-spacial-dimensional reaction-diffusion SPDEs; and we prove the existence of a SDDEs limit solution to these equations under less-than-Lipschitz conditions on the drift and the diffusion coefficients, thus extending our earlier SDDEs work to the nonzero drift case. The regularity of this solution is obtained as a by-product of the existence estimates. The uniqueness in law of our SPDEs follows, for a large class of such drifts/diffusions, as a simple extension of our recent Allen-Cahn uniqueness result. We also examine briefly, through order parameters
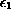and
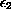multiplied by the
Laplacian and the noise, the effect of letting
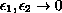at different speeds. More precisely,
it is shown that the ratio
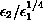determines
the behavior as
.
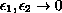