Electron. J. Diff. Eqns., Vol. 2003(2003), No. 116, pp. 1-13.
Existence and stability for some partial functional differential
equations with infinite delay
Khalil Ezzinbi
Abstract:
We study the existence, regularity, and stability of solutions for
some partial functional differential equations with infinite delay.
We assume that the linear part is not necessarily densely defined and
satisfies the Hille-Yosida condition on a Banach space
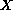 .
The nonlinear term takes its values in space larger than
.
The nonlinear term takes its values in space larger than
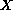 , namely
the extrapolated Favard class of the extrapolated semigroup
corresponding to the linear part. Our approach is based on the theory
of the extrapolation spaces.
, namely
the extrapolated Favard class of the extrapolated semigroup
corresponding to the linear part. Our approach is based on the theory
of the extrapolation spaces.
Submitted May 29, 2003. Published November 26, 2003.
Math Subject Classifications: 34K20, 34K30, 34K40, 45N05.
Key Words: Hille-Yosida operator, extrapolation spaces, Favard class,
regularity, partial functional differential equations,
infinite delay, mild solution, linearized stability.
Show me the
PDF file (228K),
TEX file for this article.
 |
Khalil Ezzinbi
Universite Cadi Ayyad
Faculte des Sciences Semlalia
Departement de Mathematiques
B. P. 2390, Marrakech, Morocco
email: ezzinbi@ucam.ac.ma |
|---|
Return to the EJDE web page
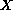 .
The nonlinear term takes its values in space larger than
.
The nonlinear term takes its values in space larger than
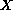 , namely
the extrapolated Favard class of the extrapolated semigroup
corresponding to the linear part. Our approach is based on the theory
of the extrapolation spaces.
, namely
the extrapolated Favard class of the extrapolated semigroup
corresponding to the linear part. Our approach is based on the theory
of the extrapolation spaces.
