In this paper we investigate the boundary eigenvalue problem
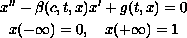
depending on the real parameter
 .
We take
.
We take
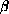 continuous
and positive and assume that
continuous
and positive and assume that
 is bounded and becomes active
and positive only when
is bounded and becomes active
and positive only when
 exceeds a threshold value
exceeds a threshold value
![$\theta \in ]0,1[$](gifs/af.gif) .
At the point
.
At the point
 we allow
we allow
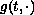 to have a jump. Additional monotonicity properties are required,
when needed. Our main discussion deals with the non-autonomous case.
In this context we prove the existence of a continuum of values
to have a jump. Additional monotonicity properties are required,
when needed. Our main discussion deals with the non-autonomous case.
In this context we prove the existence of a continuum of values
 for which this problem is solvable and we estimate the interval
of such admissible values. In the autonomous case, we show its
solvability for at most one
for which this problem is solvable and we estimate the interval
of such admissible values. In the autonomous case, we show its
solvability for at most one
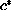 .
In the special case when
.
In the special case when
 reduces to
reduces to
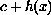 with
with
 continuous, we also give a
non-existence result, for any real
continuous, we also give a
non-existence result, for any real
 .
Our methods combine
comparison-type arguments, both for first and second order
dynamics, with a shooting technique. Some applications of the
obtained results are included.
.
Our methods combine
comparison-type arguments, both for first and second order
dynamics, with a shooting technique. Some applications of the
obtained results are included.

