Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 120, pp. 1-19.
Solvability of a (p, n-p)-type multi-point boundary-value problem
for higher-order differential equations
Yuji Liu & Weigao Ge
Abstract:
In this article, we study the differential equation
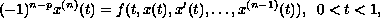
subject to the multi-point boundary conditions
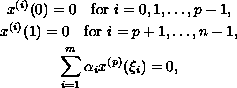
where
 .
We establish sufficient conditions for the
existence of at least one solution at resonance and another at
non-resonance. The emphasis in this paper is that
.
We establish sufficient conditions for the
existence of at least one solution at resonance and another at
non-resonance. The emphasis in this paper is that
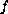 depends on
all higher-order derivatives. Examples are given to illustrate the
main results of this article.
depends on
all higher-order derivatives. Examples are given to illustrate the
main results of this article.
Submitted August 19, 2003. Published December 1, 2003.
Math Subject Classifications: 34K20, 92D25.
Key Words: Solvability, resonance, non-resonance,
multi-point boundary-value problem, higher order differential equation.
Show me the
PDF file (251K),
TEX file, and other files for this article.
 |
Yuji Liu
Department of Mathematics
Beijing Institute of Technology
Beijing, 100081, China
Department of Applied Mathematics
Hunan Institute of Technology,
Hunan, 414000, China
email: liuyuji888@sohu.com
|
|---|
| |
Weigao Ge
Department of Applied Mathematics
Beijing Institute of Technology
Beijing, 100081, China |
|---|
Return to the EJDE web page
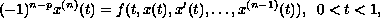
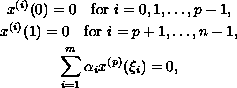
 .
We establish sufficient conditions for the
existence of at least one solution at resonance and another at
non-resonance. The emphasis in this paper is that
.
We establish sufficient conditions for the
existence of at least one solution at resonance and another at
non-resonance. The emphasis in this paper is that
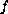 depends on
all higher-order derivatives. Examples are given to illustrate the
main results of this article.
depends on
all higher-order derivatives. Examples are given to illustrate the
main results of this article.
