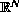
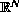
Gabriel Lopez Garza & Adolfo J. Rumbos
Abstract:
We prove the existence of weak solutions for the semilinear
elliptic problem

where
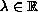 ,
,
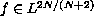 ,
,
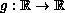 is a continuous bounded function,
and
is a continuous bounded function,
and
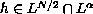 ,
,
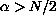 .
We assume that
.
We assume that
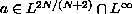 in the case of
resonance and that
in the case of
resonance and that
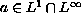 and
and
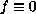 for the case of strong resonance. We prove first that the Palais-Smale
condition holds for the functional associated with the semilinear problem
using the concentration-compactness lemma of Lions. Then we prove the
existence of weak solutions by applying the saddle point theorem of
Rabinowitz for the cases of non-resonance and resonance, and a linking
theorem of Silva in the case of strong resonance. The main theorems in
this paper constitute an extension to
for the case of strong resonance. We prove first that the Palais-Smale
condition holds for the functional associated with the semilinear problem
using the concentration-compactness lemma of Lions. Then we prove the
existence of weak solutions by applying the saddle point theorem of
Rabinowitz for the cases of non-resonance and resonance, and a linking
theorem of Silva in the case of strong resonance. The main theorems in
this paper constitute an extension to
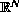 of previous results
in bounded domains by Ahmad, Lazer, and Paul [2], for the case
of resonance, and by Silva [15] in the strong resonance case.
of previous results
in bounded domains by Ahmad, Lazer, and Paul [2], for the case
of resonance, and by Silva [15] in the strong resonance case.
Submitted June 3, 2003. Published December 16, 2003.
Math Subject Classifications: 35J20.
Key Words: Resonance, strong resonance, concentration-compactness.
Show me the PDF file (302K), TEX file for this article.
 |
Gabriel Lopez Garza Dept. of Math., Claremont Graduate University Claremont California 91711, USA email: Gabriel.Lopez@cgu.edu |
|---|---|
 |
Adolfo J. Rumbos Department of Mathematics, Pomona College Claremont, California 91711, USA email: arumbos@pomona.edu |
Return to the EJDE web page