Electron. J. Diff. Eqns., Vol. 2003(2003), No. 14, pp. 1-10.
A new theorem on exponential stability of
periodic evolution families on Banach spaces
Constantin Buse & Oprea Jitianu
Abstract:
We consider a mild solution
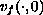 of a well-posed
inhomogeneous Cauchy problem
of a well-posed
inhomogeneous Cauchy problem
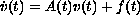 ,
,
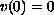
on a complex Banach space
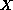 ,
where
,
where
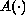 is a 1-periodic
operator-valued function. We prove that if
is a 1-periodic
operator-valued function. We prove that if
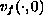 belongs to
belongs to
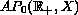 for each
for each
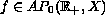 then for each
then for each
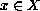 the solution of the well-posed Cauchy problem
the solution of the well-posed Cauchy problem
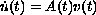 ,
,

is uniformly exponentially stable. The converse statement is
also true. Details about the space
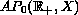 are given in the section 1, below. Our approach
is based on the spectral theory of evolution semigroups.
are given in the section 1, below. Our approach
is based on the spectral theory of evolution semigroups.
Submitted November 13, 2002. Published February 11, 2003.
Math Subject Classifications: 26D10, 34A35, 34D05, 34B15, 45M10, 47A06.
Key Words: Almost periodic functions, exponential stability,
periodic evolution families of operators, integral inequality,
differential inequality on Banach spaces.
Show me the
PDF file (216K),
TEX file for this article.
 |
Constantin Buse
Department of Mathematics
West University of Timisoara
Bd. V. Parvan 4
1900 Timisoara, Romania
e-mail: buse@hilbert.math.uvt.ro
|
|---|
 |
Oprea Jitianu
Department of Applied Mathematics
University of Craiova
Bd. A. I. Cuza 13,
1100-Craiova, Romania
e-mail: jitianu@ucv.netmasters.ro |
|---|
Return to the EJDE web page
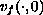 of a well-posed
inhomogeneous Cauchy problem
of a well-posed
inhomogeneous Cauchy problem 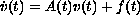 ,
,
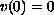
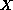 ,
where
,
where
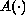 is a 1-periodic
operator-valued function. We prove that if
is a 1-periodic
operator-valued function. We prove that if
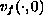 belongs to
belongs to
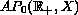 for each
for each
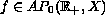 then for each
then for each
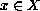 the solution of the well-posed Cauchy problem
the solution of the well-posed Cauchy problem 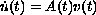 ,
,

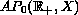 are given in the section 1, below. Our approach
is based on the spectral theory of evolution semigroups.
are given in the section 1, below. Our approach
is based on the spectral theory of evolution semigroups.

