Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 37, pp. 1-13.
Radial solutions of singular nonlinear biharmonic equations and
applications to conformal geometry
P. J. McKenna & Wolfgang Reichel
Abstract:
Positive entire solutions of the singular biharmonic equation
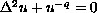 in
in
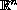 with
with
 and
and
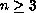 are considered. We prove that there are infinitely many radial
entire solutions with different growth rates close to quadratic.
If
are considered. We prove that there are infinitely many radial
entire solutions with different growth rates close to quadratic.
If
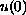 is kept fixed we show that a unique minimal entire
solution exists, which separates the entire solutions from those
with compact support. For the special case
is kept fixed we show that a unique minimal entire
solution exists, which separates the entire solutions from those
with compact support. For the special case
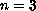 and
and
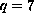 the function
the function
 is the minimal entire
solution if
is the minimal entire
solution if
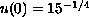 is kept fixed.
is kept fixed.
Submitted February 12, 2003. Published April 10, 2003.
Math Subject Classifications: 35J60.
Key Words: Singular biharmonic equation, conformal invariance.
Show me the
PDF file (251K),
TEX file for this article.
 |
Joe McKenna
Department of Mathematics
University of Connecticut
Storrs, CT 06269, USA
email: mckenna@math.uconn.edu
|
|---|
 |
Wolfgang Reichel
Mathematisches Institut
Universitat Basel
Rheinsprung 21, CH-4051 Basel, Switzerland
email: reichel@math.unibas.ch
|
|---|
Return to the EJDE web page
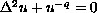 in
in
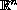 with
with
 and
and
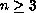 are considered. We prove that there are infinitely many radial
entire solutions with different growth rates close to quadratic.
If
are considered. We prove that there are infinitely many radial
entire solutions with different growth rates close to quadratic.
If
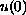 is kept fixed we show that a unique minimal entire
solution exists, which separates the entire solutions from those
with compact support. For the special case
is kept fixed we show that a unique minimal entire
solution exists, which separates the entire solutions from those
with compact support. For the special case
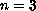 and
and
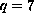 the function
the function
 is the minimal entire
solution if
is the minimal entire
solution if
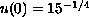 is kept fixed.
is kept fixed.

