Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 40, pp. 1-7.
Existence of solutions to higher-order discrete three-point problems
Douglas R. Anderson
Abstract:
We are concerned with the higher-order discrete three-point boundary-value
problem
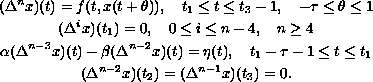
By placing certain restrictions on the nonlinearity and the distance
between boundary points, we prove the existence of at least one
solution of the boundary value problem by applying the Krasnoselskii
fixed point theorem.
Submitted August 19, 2002. Published April 15, 2003.
Math Subject Classifications: 39A10.
Key Words: Difference equations, boundary-value problem, Green's function,
fixed points, cone.
Show me the
PDF file (177K),
TEX file for this article.
 |
Douglas R. Anderson
Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA}
email: andersod@cord.edu |
|---|
Return to the EJDE web page