Electron. J. Diff. Eqns., Vol. 2003(2003), No. 42, pp. 1-10.

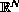
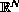
A discontinuous problem involving the p-Laplacian operator and critical exponent in $\mathbb{R}^N$

Claudianor Oliveira Alves & Ana Maria Bertone

Abstract:
Using convex analysis, we establish the existence of at least two nonnegative solutions for the quasilinear problem
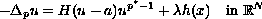
$$ -\Delta_{p}u=H(u-a)u^{p^*-1} +\lambda h(x)\quad\hbox{in }\mathbb{R}^N $$
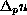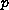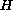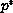where $\Delta_{p}u$ is the $p$-Laplacian operator, $H$ is the Heaviside function, $p^*$ is the Sobolev critical exponent, and 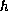$h$ is a positive function.

Submitted September 23, 2002. Published April 16, 2003.
Math Subject Classifications: 35A15, 35J60, 35H30.
Key Words: Variational methods, discontinuous nonlinearities, critical exponents.

Show me the PDF file (234K), TEX file for this article.

Claudianor Oliveira Alves
Universidade Federal de Campina Grande
Departamento de Matematica
58109-970 Campina Grande-PB, Brazil
email: coalves@dme.ufpb.br
Ana Maria Bertone
Universidade Federal da Paraiba
Departamento de Matematica
58059-900 Joao Pessoa-PB, Brazil
email: anita@mat.ufpb.br

Return to the EJDE web page