Electron. J. Diff. Eqns., Vol. 2003(2003), No. 66, pp. 1-11.
Life span of nonnegative solutions to certain quasilinear
parabolic Cauchy problems
Hendrik J. Kuiper
Abstract:
We consider the problem
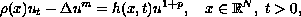
with nonnegative, nontrivial, continuous initial condition,

An integral inequality is obtained that can be used to find an
exponent
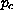 such that this problem has no nontrivial global solution
when
such that this problem has no nontrivial global solution
when
 .
This integral inequality may also be used to estimate
the maximal
.
This integral inequality may also be used to estimate
the maximal
 such that there is a solution for
such that there is a solution for
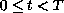 .
This is illustrated for the case
.
This is illustrated for the case
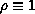 and
and
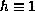 with
initial condition
with
initial condition
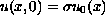 ,
,
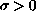 ,
by obtaining a bound of the form
,
by obtaining a bound of the form
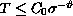 .
.
Submitted May 15, 2003. Published June 13, 2003.
Math Subject Classifications: 35K55, 35B33, 35B30.
Key Words: Nonlinear parabolic equation, blow-up, lifespan,
critical exponent.
Show me the
PDF file (236K),
TEX file for this article.
 |
Hendrik J. Kuiper
Department of Mathematics
Arizona State University
Tempe, AZ 85287-1804 USA
email: kuiper@asu.edu |
|---|
Return to the EJDE web page
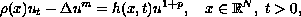

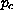 such that this problem has no nontrivial global solution
when
such that this problem has no nontrivial global solution
when
 .
This integral inequality may also be used to estimate
the maximal
.
This integral inequality may also be used to estimate
the maximal
 such that there is a solution for
such that there is a solution for
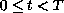 .
This is illustrated for the case
.
This is illustrated for the case
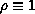 and
and
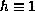 with
initial condition
with
initial condition
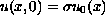 ,
,
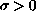 ,
by obtaining a bound of the form
,
by obtaining a bound of the form
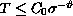 .
.
