Let
 be a time scale such that
be a time scale such that
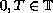 .
We consider the second order dynamic equation on a time scale
.
We consider the second order dynamic equation on a time scale

where
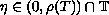 ,
and
,
and
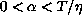 .
We apply a cone theoretic fixed point theorem
to show the existence of positive solutions.
.
We apply a cone theoretic fixed point theorem
to show the existence of positive solutions.
Eric R. Kaufmann
Abstract:
Let
 be a time scale such that
be a time scale such that
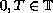 .
We consider the second order dynamic equation on a time scale
.
We consider the second order dynamic equation on a time scale

where
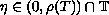 ,
and
,
and
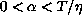 .
We apply a cone theoretic fixed point theorem
to show the existence of positive solutions.
.
We apply a cone theoretic fixed point theorem
to show the existence of positive solutions.
Submitted May 9, 2003. Published August 9, 2003.
Math Subject Classifications: 34B10, 34B15, 34G20.
Key Words: Time scale, cone, boundary-value problem, positive solutions.
Show me the PDF file (209K), TEX file for this article.
 |
Eric R. Kaufmann Department of Mathematics and Statistics University of Arkansas at Little Rock Little Rock, Arkansas 72204-1099, USA email: erkaufmann@ualr.edu |
|---|
Return to the EJDE web page