For several classes of functions including the special case
 ,
,
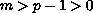 ,
we obtain Liouville
type, boundedness and symmetry results for solutions of the
non-linear
,
we obtain Liouville
type, boundedness and symmetry results for solutions of the
non-linear
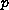 -Laplacian problem
-Laplacian problem
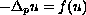 defined on the whole space
defined on the whole space
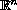 .
Suppose
.
Suppose
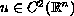 is a solution. We have that either
is a solution. We have that either (1) if
 does not change sign, then
does not change sign, then
 is a constant
(hence,
is a constant
(hence,
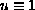 or
or
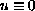 or
or
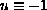 ); or
); or (2) if
 changes sign, then
changes sign, then
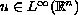 ,
moreover
,
moreover
 on
on
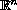 ; or
; or (3) if
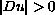 on
on
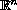 and the level set
and the level set
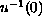 lies
on one side of a hyperplane and touches that hyperplane, i.e.,
there exists
lies
on one side of a hyperplane and touches that hyperplane, i.e.,
there exists
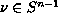 and
and
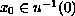 such that
such that
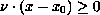 for all
for all
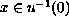 ,
then
,
then
 depends on one variable only (in the direction of
depends on one variable only (in the direction of
 ).
).
