Electron. J. Diff. Eqns., Vol. 2004(2004), No. 01, pp. 1-18.
First order linear ordinary differential equations in associative algebras
Gordon Erlebacher & Garrret E. Sobczyk
Abstract:
In this paper, we study the linear differential equation
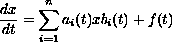
in an associative but non-commutative algebra
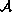 ,
where the
,
where the
 form a set of commuting
form a set of commuting
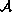 -valued
functions
expressed in a time-independent spectral basis consisting of mutually
annihilating idempotents and nilpotents. Explicit new closed solutions
are derived, and examples are presented to illustrate the theory.
-valued
functions
expressed in a time-independent spectral basis consisting of mutually
annihilating idempotents and nilpotents. Explicit new closed solutions
are derived, and examples are presented to illustrate the theory.
Submitted September 6, 2003. Published January 2, 2004.
Math Subject Classifications: 15A33, 15A66, 34G10, 39B12.
Key Words: Associative algebra, factor ring, idempotent,
differential equation, nilpotent, spectral basis, Toeplitz matrix.
Show me the
PDF file (240K),
TEX file, and other files for this article.
 |
Gordon Erlebacher
Department of Mathematics
Florida State University
Tallahassee, FL 32306, USA
email: erlebach@math.fsu.edu |
|---|
 |
Garret E. Sobczyk
Universidad de las Americas
Departamento de Fisico-Matematicas
Apartado Postal #100, Santa Catarina Martir
72820 Cholula, Pue., Mexico
email: sobczyk@mail.udlap.mx |
|---|
Return to the EJDE web page
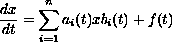
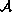 ,
where the
,
where the
 form a set of commuting
form a set of commuting
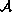 -valued
functions
expressed in a time-independent spectral basis consisting of mutually
annihilating idempotents and nilpotents. Explicit new closed solutions
are derived, and examples are presented to illustrate the theory.
-valued
functions
expressed in a time-independent spectral basis consisting of mutually
annihilating idempotents and nilpotents. Explicit new closed solutions
are derived, and examples are presented to illustrate the theory.

