Electron. J. Diff. Eqns., Vol. 2004(2004), No. 103, pp. 1-21.
A nonlinear wave equation with a nonlinear integral equation
involving the boundary value
Thanh Long Nguyen, Tien Dung Bui
Abstract:
We consider the initial-boundary value problem for the
nonlinear wave equation
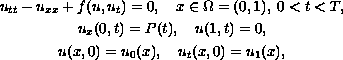
where
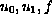 are given functions, the unknown function
are given functions, the unknown function
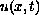 and the unknown boundary value
and the unknown boundary value
 satisfy the nonlinear integral equation
satisfy the nonlinear integral equation

where
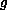 ,
,
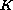 ,
,
 are given functions. We prove the existence
and uniqueness of weak solutions to this problem, and discuss
the stability of the solution with respect to the functions
are given functions. We prove the existence
and uniqueness of weak solutions to this problem, and discuss
the stability of the solution with respect to the functions
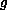 ,
,
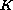 , and
, and
 .
For the proof, we use the Galerkin method.
.
For the proof, we use the Galerkin method.
Submitted January 14, 2004. Published September 3, 2004.
Math Subject Classifications: 35B30, 35L70, 35Q72.
Key Words: Galerkin method; integrodifferential equations;
Schauder fixed point theorem; weak solutions;
stability of the solutions
Show me the
PDF file (323K),
TEX file for this article.
 |
Thanh Long Nguyen
Department of Mathematics and Computer Science
University of Natural Science
Vietnam National University HoChiMinh City
227 Nguyen Van Cu Str., Dist.5, HoChiMinh City, Vietnam
email: longnt@hcmc.netnam.vn |
|---|
 |
Tien Dung Bui
Department of Mathematics
University of Architecture of HoChiMinh City
196 Pasteur Str., Dist. 3, HoChiMinh City, Vietnam |
|---|
Return to the EJDE web page
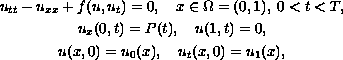
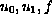 are given functions, the unknown function
are given functions, the unknown function
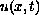 and the unknown boundary value
and the unknown boundary value
 satisfy the nonlinear integral equation
satisfy the nonlinear integral equation

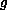 ,
,
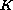 ,
,
 are given functions. We prove the existence
and uniqueness of weak solutions to this problem, and discuss
the stability of the solution with respect to the functions
are given functions. We prove the existence
and uniqueness of weak solutions to this problem, and discuss
the stability of the solution with respect to the functions
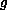 ,
,
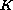 , and
, and
 .
For the proof, we use the Galerkin method.
.
For the proof, we use the Galerkin method.

