In this work we study the problem
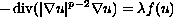
in the unit ball of
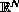 , with
, with
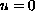 on the boundary,
where
on the boundary,
where
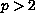 , and
, and
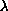 is a real parameter.
We assume that the nonlinearity
is a real parameter.
We assume that the nonlinearity
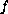 has a zero
has a zero
 of order
of order
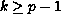 .
Our main contribution is showing that there exists a unique
positive solution of this problem for large enough
.
Our main contribution is showing that there exists a unique
positive solution of this problem for large enough
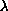 and maximum close to
and maximum close to
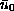 .
This will be achieved by
means of a linearization technique, and we also prove the
new result that the inverse of the
.
This will be achieved by
means of a linearization technique, and we also prove the
new result that the inverse of the
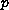 -Laplacian
is differentiable
around positive solutions.
-Laplacian
is differentiable
around positive solutions.
