Electron. J. Diff. Eqns.,
Vol. 2004(2004), No. 111, pp. 1-10
Nontrivial solution for a three-point boundary-value problem
Yong-Ping Sun
Abstract:
In this paper, we study the existence of nontrivial
solutions for the second-order three-point boundary-value problem
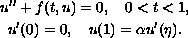
where
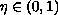 ,
,
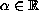 ,
,
![$f\in C([0,1]\times \mathbb{R},\mathbb{R})$](gifs/ad.gif) .
Under certain growth conditions on the nonlinearity
.
Under certain growth conditions on the nonlinearity
 and by using Leray-Schauder nonlinear alternative,
sufficient conditions for the existence of nontrivial solution
are obtained. We illustrate the results obtained with some examples.
and by using Leray-Schauder nonlinear alternative,
sufficient conditions for the existence of nontrivial solution
are obtained. We illustrate the results obtained with some examples.
Submitted June 15, 2004. Published September 22, 2004.
Math Subject Classifications: 34B10, 34B15.
Key Words: Three-point boundary-value problem; nontrivial solution;
Leray-Schauder nonlinear alternative.
Show me the
PDF file (198K),
TEX file for this article.
 |
Yong-Ping Sun
Department of Fundamental Courses
Hangzhou Radio and TV University
Hangzhou, Zhejiang 310012, China
email: syp@mail.hzrtvu.edu.cn |
|---|
Return to the EJDE web page
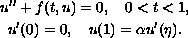
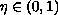 ,
,
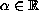 ,
,
![$f\in C([0,1]\times \mathbb{R},\mathbb{R})$](gifs/ad.gif) .
Under certain growth conditions on the nonlinearity
.
Under certain growth conditions on the nonlinearity
 and by using Leray-Schauder nonlinear alternative,
sufficient conditions for the existence of nontrivial solution
are obtained. We illustrate the results obtained with some examples.
and by using Leray-Schauder nonlinear alternative,
sufficient conditions for the existence of nontrivial solution
are obtained. We illustrate the results obtained with some examples.
