We consider the nonlinear equation
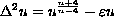
with
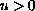 in
in
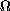 and
and
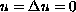 on
on
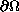 .
Where
.
Where
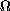 is a smooth bounded domain in
is a smooth bounded domain in
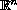 ,
,
 ,
and
,
and
 is a small positive parameter.
We study the existence of solutions which
concentrate around one or two points of
is a small positive parameter.
We study the existence of solutions which
concentrate around one or two points of
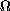 .
We show that this problem has no solutions that concentrate
around a point of
.
We show that this problem has no solutions that concentrate
around a point of
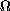 as
as
 approaches 0.
In contrast to this, we construct a domain for which
there exists a family of solutions which blow-up and concentrate
in two different points of
approaches 0.
In contrast to this, we construct a domain for which
there exists a family of solutions which blow-up and concentrate
in two different points of
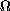 as
as
 approaches 0.
approaches 0.
