Electron. J. Diff. Eqns., Vol. 2004(2004), No. 122, pp. 1-7.
Normal forms for singularities of one dimensional
holomorphic vector fields
Antonio Garijo, Armengol Gasull, Xavier Jarque
Abstract:
We study the normal form of the ordinary differential equation
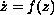 ,
,
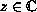 ,
,
in a neighbourhood of a point
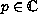 ,
where
,
where
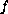 is a one-dimensional holomorphic function
in a punctured neighbourhood of
is a one-dimensional holomorphic function
in a punctured neighbourhood of
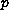 .
Our results include all cases except when
.
Our results include all cases except when
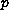 is an essential singularity. We treat all the other
situations, namely when
is an essential singularity. We treat all the other
situations, namely when
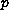 is a regular point, a pole or a zero of
order
is a regular point, a pole or a zero of
order
 .
Our approach is based on a formula that uses the flow
associated with the differential equation to search for the change of
variables that gives the normal form.
.
Our approach is based on a formula that uses the flow
associated with the differential equation to search for the change of
variables that gives the normal form.
Submitted June 23, 2004. Published October 15, 2004.
Math Subject Classifications: 34C20, 34A34, 32A10, 37C10.
Key Words: Meromorphic vector field; holomorphic vector field; normal form.
Show me the
PDF file (209K),
TEX file for this article.
 |
Antonio Garijo
Dep. d'Eng. Informática i Matemátiques
Universitat Rovira i Virgili
Av. Pa&iunl;sos Catalans, 26
43007 Tarragona, Spain
email: agarijo@etse.urv.es |
|---|
 |
Armengol Gasull
Dept. de Matemátiques
Universitat Autónoma de Barcelona
Edifici C, 08193 Bellaterra, Barcelona, Spain
email: gasull@mat.uab.es
|
|---|
 |
Xavier Jarque
Dep. de Matemáatica Aplicada i Análisi
Universitat de Barcelona
Gran Via 585
08007 Barcelona, Spain
email: xavier.jarque@ub.edu |
|---|
Return to the EJDE web page
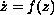 ,
,
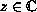 ,
, 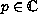 ,
where
,
where
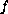 is a one-dimensional holomorphic function
in a punctured neighbourhood of
is a one-dimensional holomorphic function
in a punctured neighbourhood of
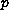 .
Our results include all cases except when
.
Our results include all cases except when
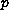 is an essential singularity. We treat all the other
situations, namely when
is an essential singularity. We treat all the other
situations, namely when
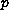 is a regular point, a pole or a zero of
order
is a regular point, a pole or a zero of
order
 .
Our approach is based on a formula that uses the flow
associated with the differential equation to search for the change of
variables that gives the normal form.
.
Our approach is based on a formula that uses the flow
associated with the differential equation to search for the change of
variables that gives the normal form.


