To account for an external magnetic field in a Hamiltonian of a quantum system on a manifold (modelled here by a subelliptic Dirichlet form), one replaces the the momentum operator
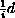 in the subelliptic symbol
by
in the subelliptic symbol
by
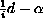 ,
where
,
where
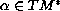 is called a
magnetic potential for the magnetic field
is called a
magnetic potential for the magnetic field
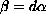 .
.We prove existence of ground state solutions (Sobolev minimizers) for nonlinear Schrodinger equation associated with such Hamiltonian on a generally, non-compact Riemannian manifold, generalizing the existence result of Esteban-Lions [5] for the nonlinear Schrödinger equation with a constant magnetic field on
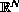 and the existence
result of [6] for a similar problem on manifolds
without a magnetic field. The counterpart of a constant magnetic
field is the magnetic field, invariant with respect to a subgroup
of isometries. As an example to the general statement we calculate
the invariant magnetic fields in the Hamiltonians associated with
the Kohn Laplacian and for the Laplace-Beltrami operator on the
Heisenberg group.
and the existence
result of [6] for a similar problem on manifolds
without a magnetic field. The counterpart of a constant magnetic
field is the magnetic field, invariant with respect to a subgroup
of isometries. As an example to the general statement we calculate
the invariant magnetic fields in the Hamiltonians associated with
the Kohn Laplacian and for the Laplace-Beltrami operator on the
Heisenberg group.
