Electron. J. Diff. Eqns., Vol. 2004(2004), No. 124, pp. 1-17.
Anti-periodic solutions for second order differential inclusions
Jean-Francois Couchouron, Radu Precup
Abstract:
In this paper, we extend the existence results presented in
[9] for
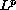 spaces to operator inclusions of Hammerstein
type in
spaces to operator inclusions of Hammerstein
type in
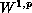 spaces.
We also show an application of our
results to anti-periodic boundary-value problems of second-order
differential equations with nonlinearities depending on
spaces.
We also show an application of our
results to anti-periodic boundary-value problems of second-order
differential equations with nonlinearities depending on
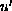 .
.
Submitted May 10, 2004. Published October 18, 2004.
Math Subject Classifications: 45N05, 47J35, 34G25.
Key Words: Anti-periodic solution; nonlinear boundary-value problem;
dissipative operator; multivalued mapping; fixed point.
Show me the
PDF file (296K),
TEX file, and other files for this article.
 |
Jean-Francois Couchouron
Université de Metz
Mathématiques INRIA Lorraine,
Ile du Saulcy, 57045 Metz, France
e-mail: Jean-Francois.Couchouron@loria.fr |
|---|
 |
Radu Precup
University Babes-Bolyai,
Faculty of Mathematics and Computer Science,
3400 Cluj, Romania
e-mail: r.precup@math.ubbcluj.ro |
|---|
Return to the EJDE web page
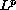 spaces to operator inclusions of Hammerstein
type in
spaces to operator inclusions of Hammerstein
type in
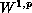 spaces.
We also show an application of our
results to anti-periodic boundary-value problems of second-order
differential equations with nonlinearities depending on
spaces.
We also show an application of our
results to anti-periodic boundary-value problems of second-order
differential equations with nonlinearities depending on
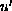 .
.

