Electron. J. Diff. Eqns., Vol. 2004(2004), No. 16, pp. 1-11.
The eigenvalue problem for a singular quasilinear elliptic equation
Benjin Xuan
Abstract:
We show that many results about the eigenvalues and
eigenfunctions of a quasilinear elliptic equation
in the non-singular case can be extended to the singular case.
Among these results, we have the first eigenvalue is associated
to a
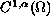 eigenfunction which is positive and
unique (up to a multiplicative constant), that is, the first
eigenvalue is simple. Moreover the first eigenvalue is isolated
and is the unique positive eigenvalue associated to a non-negative
eigenfunction. We also prove some variational properties of the
second eigenvalue.
eigenfunction which is positive and
unique (up to a multiplicative constant), that is, the first
eigenvalue is simple. Moreover the first eigenvalue is isolated
and is the unique positive eigenvalue associated to a non-negative
eigenfunction. We also prove some variational properties of the
second eigenvalue.
Submitted August 15, 2003. Published February 6, 2004.
Math Subject Classifications: 35J60.
Key Words: Singular quasilinear elliptic equation, eigenvalue problem,
Caffarelli-Kohn-Nirenberg inequality.
Show me the
PDF file (225K),
TEX file for this article.
 |
Benjin Xuan
Department of Mathematics
University of Science and Technology of China
Dept. de Matematicas, Universidad Nacional
Bogota, Colombia
e-mail: wenyuanxbj@yahoo.com |
|---|
Return to the EJDE web page
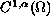 eigenfunction which is positive and
unique (up to a multiplicative constant), that is, the first
eigenvalue is simple. Moreover the first eigenvalue is isolated
and is the unique positive eigenvalue associated to a non-negative
eigenfunction. We also prove some variational properties of the
second eigenvalue.
eigenfunction which is positive and
unique (up to a multiplicative constant), that is, the first
eigenvalue is simple. Moreover the first eigenvalue is isolated
and is the unique positive eigenvalue associated to a non-negative
eigenfunction. We also prove some variational properties of the
second eigenvalue.
