Electron. J. Diff. Eqns., Vol. 2004(2004), No. 18, pp. 1-12.

Existence of solutions to second order ordinary differential equations having finite limits at $\pm\infty$

Cezar Avramescu & Cristian Vladimirescu

Abstract:
In this article, we study the boundary-value problem
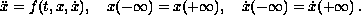
$$ \ddot{x}=f(t,x,\dot{x}), \quad x(-\infty )=x(+\infty ), \quad \dot{x}(-\infty) = \dot{x}(+\infty ) =0\,. $$
Under adequate hypotheses and using the Bohnenblust-Karlin fixed point theorem for multivalued mappings, we establish the existence of solutions.

Submitted February 14, 2003. Published February 9, 2004.
Math Subject Classifications: 34B15, 34B40, 34C37, 54C60.
Key Words: Nonlinear boundary-value problem, set-valued mappings, boundary-value problems on infinite intervals.

Show me the PDF file (211K), TEX file, and other files for this article.

Cezar Avramescu
Centre for Nonlinear Analysis and its Applications
University of Craiova, Al.I. Cuza Street, No. 13
Craiova RO-200585, Romania
email: zarce@central.ucv.ro   cezaravramescu@hotmail.com
Cristian Vladimirescu
Department of Mathematics, University of Craiova
Al.I. Cuza Street, No. 13
Craiova RO-200585, Romania
email: cvladi@central.ucv.ro   vladimirescucris@hotmail.com

Return to the EJDE web page