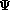 -bounded solutions for a system
of differential equations
-bounded solutions for a system
of differential equations
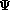 -bounded solutions for a system
of differential equations
-bounded solutions for a system
of differential equations
Aurel Diamandescu
Abstract:
In this article, we present a necessary and sufficient condition for
the existence of solutions to the linear nonhomogeneous system
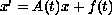 .
Under the condition stated, for every Lebesgue
.
Under the condition stated, for every Lebesgue
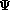 -integrable
function
-integrable
function
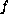 there is at least one
there is at least one
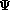 -bounded
solution on the interval
-bounded
solution on the interval
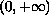 .
.
Submitted March 5, 2004. Published April 23, 2004.
Math Subject Classifications: 34D05, 34C11.
Key Words:
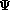 -bounded,
Lebesgue
-bounded,
Lebesgue
 -integrable
function.
-integrable
function.
Show me the PDF file (175K), TEX file for this article.
 |
Aurel Diamandescu Department of Applied Mathematics University of Craiova, 13 "Al. I. Cuza" st. 200.585 Craiova, Romania email: adiamandescu@central.ucv.ro |
|---|
Return to the EJDE web page