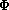 -Laplacian when
-Laplacian when
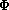 is a sup - multiplicative - like function
is a sup - multiplicative - like function
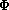 -Laplacian when
-Laplacian when
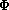 is a sup - multiplicative - like function
is a sup - multiplicative - like function
George L. Karakostas
Abstract:
We provide sufficient conditions for the existence of positive
solutions of a boundary-value problem for a one dimensional
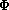 -Laplacian
ordinary differential equation with deviating
arguments, where
-Laplacian
ordinary differential equation with deviating
arguments, where
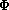 is a sup-multiplicative-like function
(in a sense introduced here) and the boundary conditions include
nonlinear expressions at the end points. For this end, we use
the Krasnoselskii fixed point theorem in a cone. The results
obtained improve and generalize known results in [17] and
elsewhere.
is a sup-multiplicative-like function
(in a sense introduced here) and the boundary conditions include
nonlinear expressions at the end points. For this end, we use
the Krasnoselskii fixed point theorem in a cone. The results
obtained improve and generalize known results in [17] and
elsewhere.
Submitted February 5, 2004. Published May 4, 2004.
Math Subject Classifications: 34B15, 34B18.
Key Words: Boundary value problems, positive solutions,
Krasnoselskii's fixed point theorem.
Show me the PDF file (233K), TEX file, and other files for this article.
 |
George L. Karakostas Department of Mathematics University of Ioannina, 451 10 Ioannina, Greece email: gkarako@cc.uoi.gr |
Return to the EJDE web page