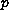 -Laplacian in
-Laplacian in
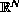
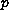 -Laplacian in
-Laplacian in
Benedicte Alziary, Jacqueline Fleckinger, Peter Takac
Abstract:
The solvability of the resonant Cauchy problem
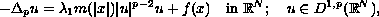
in the entire Euclidean space
\mathbb{R}^N
(
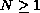 ) is
investigated as a part of the Fredholm alternative at the first
(smallest) eigenvalue
) is
investigated as a part of the Fredholm alternative at the first
(smallest) eigenvalue
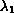 of the positive
of the positive
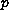 -Laplacian
-Laplacian
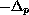 on
on
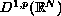 relative to the weight
relative to the weight
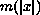 . Here,
. Here,
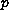 stands for the
stands for the
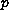 -Laplacian,
-Laplacian,
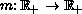 is a weight
function assumed to be radially symmetric,
is a weight
function assumed to be radially symmetric,
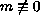 in
in
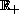 , and
, and
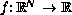 is a
given function satisfying a suitable integrability condition.
The weight
is a
given function satisfying a suitable integrability condition.
The weight
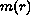 is assumed to be bounded and to decay fast enough
as
is assumed to be bounded and to decay fast enough
as
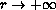 . Let
. Let
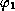 denote the (positive)
eigenfunction associated with the (simple) eigenvalue
denote the (positive)
eigenfunction associated with the (simple) eigenvalue
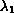 of
of
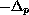 .
If
.
If
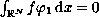 ,
we show that problem has at least one solution
,
we show that problem has at least one solution
 in the completion
in the completion
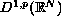 of
of
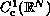 endowed with the norm
endowed with the norm
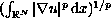 .
To establish this existence result, we employ a saddle point method
if
.
To establish this existence result, we employ a saddle point method
if
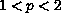 , and an improved Poincare
inequality if
, and an improved Poincare
inequality if
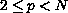 .
We use weighted Lebesgue and Sobolev spaces with
weights depending on
.
We use weighted Lebesgue and Sobolev spaces with
weights depending on
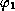 .
The asymptotic behavior of
.
The asymptotic behavior of
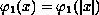 as
as
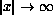 plays a crucial role.
plays a crucial role.
Submitted March 19, 2004. Published May 26, 2004.
Math Subject Classifications: 35P30, 35J20, 47J10, 47J30
Key Words: p-Laplacian, degenerate quasilinear Cauchy problem,
Fredholm alternative, (p-1)-homogeneous problem at resonance,
saddle point geometry, improved Poincare inequality,
second-order Taylor formula.
Show me the PDF file (480K), TEX file, and other files for this article.
| Benedicte Alziary CEREMATH & UMR MIP Universite Toulouse 1 - Sciences Sociales 21 allees de Brienne, F-31042 Toulouse Cedex, France email: alziary@univ-tlse1.fr | |
 |
Jacqueline Fleckinger CEREMATH & UMR MIP Universite Toulouse 1 - Sciences Sociales 21 allees de Brienne, F-31042 Toulouse Cedex, France e-mail: jfleck@univ-tlse1.fr |
 |
Peter Takac Fachbereich Mathematik, Universitat Rostock Universitatsplatz 1, D-18055 Rostock, Germany email: peter.takac@mathematik.uni-rostock.de |
Return to the EJDE web page