Electron. J. Diff. Eqns., Vol. 2004(2004), No. 98, pp. 1-28.
Structural stability of polynomial second order differential
equations with periodic coefficients
Adolfo W. Guzman
Abstract:
This work characterizes the structurally stable second order
differential equations of the form
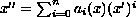 where
where
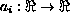 are
are
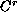 periodic functions.
These equations have naturally the cylinder
periodic functions.
These equations have naturally the cylinder
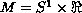 as the phase space and are associated to the vector fields
as the phase space and are associated to the vector fields
 ,
where
,
where
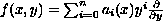 .
.
We apply a compactification to
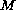 as well as to
as well as to
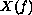 to
study the behavior at infinity. For
to
study the behavior at infinity. For
 ,
we define a set
,
we define a set
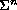 of
of
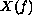 that is open and dense and characterizes
the class of structural differential equations as above.
that is open and dense and characterizes
the class of structural differential equations as above.
Submitted April 29, 2004. Published August 9, 2004.
Math Subject Classifications: 37C20.
Key Words: Singularity at infinity; compactification; structural stability;
second order differential equation.
Show me the
PDF file (499K),
TEX file for this article.
 |
Adolfo W. Guzman
Departamento de Matematica
Universidade Federal de Vicosa
Campus Universitario CEP 36571-000. Vicosa - MG. Brasil
email: guzman@ime.usp.br guzman@ufv.br |
|---|
Return to the EJDE web page
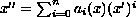 where
where
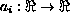 are
are
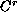 periodic functions.
These equations have naturally the cylinder
periodic functions.
These equations have naturally the cylinder
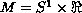 as the phase space and are associated to the vector fields
as the phase space and are associated to the vector fields  ,
where
,
where 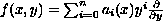 .
. 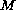 as well as to
as well as to
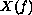 to
study the behavior at infinity. For
to
study the behavior at infinity. For
 ,
we define a set
,
we define a set
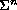 of
of
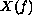 that is open and dense and characterizes
the class of structural differential equations as above.
that is open and dense and characterizes
the class of structural differential equations as above.
