

Daniela Visetti
Abstract:
In this paper, we study the nonlinear eigenvalue field equation

where
 is a function from
is a function from
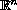 to
to
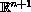 with
with
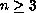 ,
,
 is a positive parameter and
is a positive parameter and
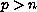 .
We find a multiplicity of solutions, symmetric with
respect to an action of the orthogonal group
.
We find a multiplicity of solutions, symmetric with
respect to an action of the orthogonal group
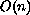 :
For any
:
For any
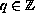 we prove the existence of finitely many
pairs
we prove the existence of finitely many
pairs
 solutions for
solutions for
 sufficiently small,
where
sufficiently small,
where
 is
symmetric and has topological charge
is
symmetric and has topological charge
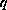 .
The multiplicity of our solutions can be as large as desired,
provided that the singular point of
.
The multiplicity of our solutions can be as large as desired,
provided that the singular point of
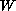 and
and
 are
chosen accordingly.
are
chosen accordingly.
Submitted October 22, 2004. Published January 2, 2005.
Math Subject Classifications: 35Q55, 45C05.
Key Words: Nonlinear Schrodinger equations; nonlinear eigenvalue problems.
Show me the PDF file (334K), TEX file for this article.
 |
Daniela Visetti Dipartimento di Matematica Applicata "U. Dini", Università degli studi di Pisa via Bonanno Pisano 25/B, 56126 Pisa, Italy email: visetti@mail.dm.unipi.it |
|---|
Return to the EJDE web page