Electron. J. Diff. Eqns., Vol. 2005(2005), No. 08, pp. 1-10.
Strong resonance problems for the one-dimensional p-Laplacian
Jiri Bouchala
Abstract:
We study the existence of the weak solution of the
nonlinear boundary-value problem
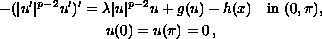
where
 and
and
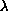 are real numbers,
are real numbers,
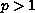 ,
,
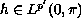 (
(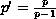 )
and the nonlinearity
)
and the nonlinearity
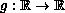 is a continuous function of the
Landesman-Lazer type. Our sufficiency conditions generalize the
results published previously about the solvability of this problem.
is a continuous function of the
Landesman-Lazer type. Our sufficiency conditions generalize the
results published previously about the solvability of this problem.
Submitted June 21, 2004. Published January 5, 2005.
Math Subject Classifications: 34B15, 34L30, 47J30.
Key Words: p-Laplacian; resonance at the eigenvalues;
Landesman-Lazer type conditions.
Show me the
PDF file (227K),
TEX file for this article.
 |
Jirí Bouchala
Department of Applied Mathematics
VSB-Technical University Ostrava, Czech republic
email: jiri.bouchala@vsb.cz |
|---|
Return to the EJDE web page
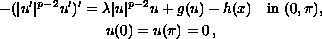
 and
and
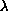 are real numbers,
are real numbers,
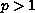 ,
,
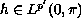 (
(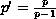 )
and the nonlinearity
)
and the nonlinearity
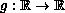 is a continuous function of the
Landesman-Lazer type. Our sufficiency conditions generalize the
results published previously about the solvability of this problem.
is a continuous function of the
Landesman-Lazer type. Our sufficiency conditions generalize the
results published previously about the solvability of this problem.
