We develop the existence, uniqueness, continuity, stability, and scattering theory for energy-critical nonlinear Schrodinger equations in dimensions
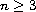 ,
for solutions which have large,
but finite, energy and large, but finite, Strichartz norms.
For dimensions
,
for solutions which have large,
but finite, energy and large, but finite, Strichartz norms.
For dimensions
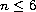 ,
this theory is a standard extension
of the small data well-posedness theory based on iteration in
Strichartz spaces. However, in dimensions
,
this theory is a standard extension
of the small data well-posedness theory based on iteration in
Strichartz spaces. However, in dimensions
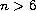 there is an
obstruction to this approach because of the subquadratic nature
of the nonlinearity (which makes the derivative of the nonlinearity
non-Lipschitz). We resolve this by iterating in exotic Strichartz
spaces instead. The theory developed here will be applied in a
subsequent paper of the second author, [21],
to establish global well-posedness and scattering for the
defocusing energy-critical equation for large energy data.
there is an
obstruction to this approach because of the subquadratic nature
of the nonlinearity (which makes the derivative of the nonlinearity
non-Lipschitz). We resolve this by iterating in exotic Strichartz
spaces instead. The theory developed here will be applied in a
subsequent paper of the second author, [21],
to establish global well-posedness and scattering for the
defocusing energy-critical equation for large energy data.

