Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 127, pp. 1-7.
Eigenvalues and symmetric positive solutions for a
three-point boundary-value problem
Yongping Sun
Abstract:
In this paper, we consider the
second-order three-point boundary-value problem
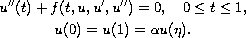
Under suitable conditions and using Schauder fixed point
theorem, we prove the existence of at least one symmetric positive
solution. We also study the existence of positive
eigenvalues for this problem. We emphasis the
highest-order derivative occurs nonlinearly in our problem.
Submitted September 15, 2005. Published November 23, 2005.
Math Subject Classifications: 34B10, 34B15.
Key Words: Symmetric positive solution;
three-point boundary-value problem;
Schauder fixed point theorem; eigenvalue.
Show me the
PDF file (177K),
TEX file for this article.
 |
Yongping Sun
Department of Fundamental Courses
Hangzhou Radio & TV University
Hangzhou, Zhejiang 310012, China
email: sunyongping@126.com |
|---|
Return to the EJDE web page