Electron. J. Diff. Eqns., Vol. 2005(2005), No. 138, pp. 1-18.
Nonlinear Kirchhoff-Carrier wave equation in a unit membrane with
mixed homogeneous boundary conditions
Nguyen Thanh Long
Abstract:
In this paper we consider the nonlinear wave equation problem
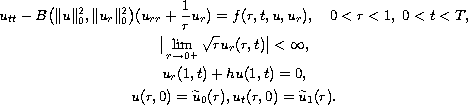
To this problem, we associate a linear recursive scheme for which the
existence of a local and unique weak solution is proved, in weighted
Sobolev using standard compactness arguments. In the latter part, we give
sufficient conditions for quadratic convergence to the solution of the
original problem, for an autonomous right-hand side independent on
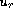 and a coefficient function
and a coefficient function
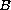 of the form
of the form
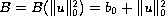 with
with
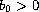 .
.
Submitted August 3, 2004. Published December 1, 2005.
Math Subject Classifications: 35L70, 35Q72.
Key Words: Nonlinear wave equation; Galerkin method; quadratic convergence;
weighted Sobolev spaces.
Show me the
PDF file (308K),
TEX file for this article.
 |
Nguyen Thanh Long
Department of Mathematics and Computer Science
University of Natural Science
Vietnam National University HoChiMinh City
227 Nguyen Van Cu Str., Dist. 5
Hochiminh City, Vietnam
email: longnt@hcmc.netnam.vn longnt2@gmail.com
|
|---|
Return to the EJDE web page
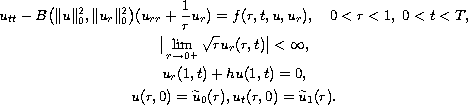
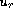 and a coefficient function
and a coefficient function
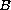 of the form
of the form
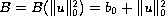 with
with
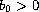 .
.
