Electron. J. Diff. Eqns., Vol. 2005(2005), No. 37, pp. 1-16.
Asymptotic shape of solutions to nonlinear eigenvalue problems
Tetsutaro Shibata
Abstract:
We consider the nonlinear eigenvalue problem
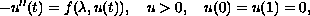
where
 is a parameter. It is known that under some
conditions on
is a parameter. It is known that under some
conditions on
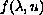 ,
the shape of the solutions associated with
,
the shape of the solutions associated with
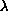 is almost `box' when
is almost `box' when
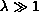 .
The purpose of this paper is to study precisely the asymptotic shape of
the solutions as
.
The purpose of this paper is to study precisely the asymptotic shape of
the solutions as
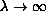 from a standpoint of
from a standpoint of
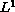 -framework.
To do this, we establish the asymptotic formulas for
-framework.
To do this, we establish the asymptotic formulas for
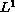 -norm
of the solutions as
-norm
of the solutions as
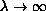 .
.
Submitted January 11, 2005. Published March 29, 2005.
Math Subject Classifications: 34B15.
Key Words: Asymptotic formula;
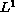 -norm; simple pendulum; logistic equation
-norm; simple pendulum; logistic equation
Show me the
PDF file (247K),
TEX file for this article.
 |
Tetsutaro Shibata
Department of Applied Mathematics
Graduate School of Engineering
Hiroshima University
Higashi-Hiroshima, 739-8527, Japan
email: shibata@amath.hiroshima-u.ac.jp
|
|---|
Return to the EJDE web page
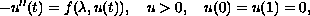
 is a parameter. It is known that under some
conditions on
is a parameter. It is known that under some
conditions on
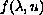 ,
the shape of the solutions associated with
,
the shape of the solutions associated with
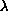 is almost `box' when
is almost `box' when
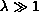 .
The purpose of this paper is to study precisely the asymptotic shape of
the solutions as
.
The purpose of this paper is to study precisely the asymptotic shape of
the solutions as
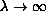 from a standpoint of
from a standpoint of
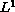 -framework.
To do this, we establish the asymptotic formulas for
-framework.
To do this, we establish the asymptotic formulas for
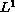 -norm
of the solutions as
-norm
of the solutions as
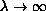 .
.
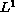 -norm; simple pendulum; logistic equation
-norm; simple pendulum; logistic equation
