In the recent papers [8] and [10] a class of Caratheodory functions
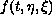 rapidly sign-changing
near the boundary point
rapidly sign-changing
near the boundary point
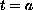 ,
has been constructed so that the
equation
,
has been constructed so that the
equation
 in
in
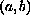 admits continuous
bounded solutions
admits continuous
bounded solutions
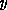 whose graphs
whose graphs
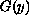 do not possess a finite
length. In this paper, the same class of functions
do not possess a finite
length. In this paper, the same class of functions
 will be given, but with slightly different input data compared to
those from the previous papers, such that the graph
will be given, but with slightly different input data compared to
those from the previous papers, such that the graph
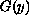 of each solution
of each solution
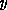 is a rectifiable curve in
is a rectifiable curve in
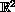 . Moreover,
there is a positive constant which does not depend on
. Moreover,
there is a positive constant which does not depend on
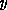 so that
so that
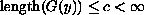 .
.
