Electron. J. Diff. Eqns., Vol. 2005(2005), No. 50, pp. 1-10.
Existence of viable solutions for nonconvex
differential inclusions
Messaoud Bounkhel, Tahar Haddad
Abstract:
We show the existence result of viable solutions to the
differential inclusion
![$$\displaylines{
\dot x(t)\in G(x(t))+F(t,x(t)) \cr
x(t)\in S \quad \hbox{on } [0,T],
}$$](gifs/aa.gif)
where
![$F: [0,T]\times H\to H$](gifs/ab.gif)
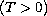 is a continuous
set-valued mapping,
is a continuous
set-valued mapping,
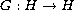 is a Hausdorff upper
semi-continuous set-valued mapping such that
is a Hausdorff upper
semi-continuous set-valued mapping such that
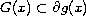 , where
, where
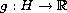 is a regular
and locally Lipschitz function and
is a regular
and locally Lipschitz function and
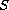 is a ball, compact
subset in a separable Hilbert space
is a ball, compact
subset in a separable Hilbert space
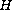 .
.
Submitted December 26, 2004. Published May 11, 2005.
Math Subject Classifications: 34A60, 34G25, 49J52, 49J53.
Key Words: Uniformly regular functions; normal cone;
nonconvex differential inclusions.
Show me the
PDF file (229K),
TEX file for this article.
 |
Messaoud Bounkhel
King Saud University, College of Science
Department of Mathematics
Riyadh 11451, Saudi Arabia
email: bounkhel@ksu.edu.sa
|
|---|
 |
Tahar Haddad
University of Jijel
Department of Mathematics
B.P. 98, Ouled Aissa, Jijel, Algeria
email: haddadtr2000@yahoo.fr
|
|---|
Return to the EJDE web page
![$$\displaylines{
\dot x(t)\in G(x(t))+F(t,x(t)) \cr
x(t)\in S \quad \hbox{on } [0,T],
}$$](gifs/aa.gif)
![$F: [0,T]\times H\to H$](gifs/ab.gif)
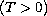 is a continuous
set-valued mapping,
is a continuous
set-valued mapping,
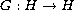 is a Hausdorff upper
semi-continuous set-valued mapping such that
is a Hausdorff upper
semi-continuous set-valued mapping such that
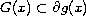 , where
, where
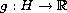 is a regular
and locally Lipschitz function and
is a regular
and locally Lipschitz function and
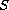 is a ball, compact
subset in a separable Hilbert space
is a ball, compact
subset in a separable Hilbert space
 .
.

