We study the following quasilinear problem with nonlinear boundary conditions
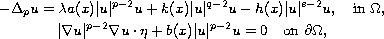
where
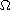 is an unbounded domain in
is an unbounded domain in
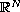 with a noncompact and smooth boundary
with a noncompact and smooth boundary
 ,
,
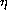 denotes
the unit outward normal vector on
denotes
the unit outward normal vector on
 ,
,
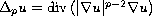 is the
is the
 -Laplacian,
-Laplacian,
 ,
,
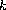 ,
,
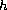 and
and
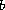 are nonnegative essentially
bounded functions,
are nonnegative essentially
bounded functions,
 and
and
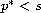 . The properties of the first eigenvalue
. The properties of the first eigenvalue
 and the associated eigenvectors of the
related eigenvalue problem are examined. Then it is shown that if
and the associated eigenvectors of the
related eigenvalue problem are examined. Then it is shown that if
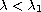 ,
the original problem admits an infinite
number of solutions one of which is nonnegative, while if
,
the original problem admits an infinite
number of solutions one of which is nonnegative, while if
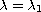 it admits at least one nonnegative solution.
Our approach is variational in character.
it admits at least one nonnegative solution.
Our approach is variational in character.
