Electron. J. Diff. Eqns., Vol. 2005(2005), No. 63, pp. 1-22.
Quasi-geostrophic equations with initial data in Banach
spaces of local measures
Sadek Gala
Abstract:
This paper studies the well posedness of the initial value problem for the
quasi-geostrophic type equations
![$$\displaylines{
\partial_{t}\theta+u\nabla\theta+( -\Delta) ^{\gamma}\theta =0
\quad \hbox{on }\mathbb{R}^{d}\times] 0,+\infty[\cr
\theta( x,0) =\theta_{0}(x), \quad x\in\mathbb{R}^{d}
}$$](gifs/aa.gif)
where
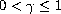 is a fixed parameter and the velocity field
is a fixed parameter and the velocity field
 is divergence free; i.e.,
is divergence free; i.e.,
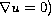 .
The initial data
.
The initial data
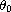 is taken in Banach
spaces of local measures (see text for the definition), such as Multipliers,
Lorentz and Morrey-Campanato spaces. We will focus on the subcritical case
is taken in Banach
spaces of local measures (see text for the definition), such as Multipliers,
Lorentz and Morrey-Campanato spaces. We will focus on the subcritical case
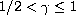 and we analyse the well-posedness of the
system in three basic spaces:
and we analyse the well-posedness of the
system in three basic spaces:
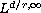 ,
,
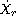 and
and
 ,
when the
solution is global for sufficiently small initial data. Furtheremore, we
prove that the solution is actually smooth. Mild solutions are obtained in
several spaces with the right homogeneity to allow the existence of
self-similar solutions.
,
when the
solution is global for sufficiently small initial data. Furtheremore, we
prove that the solution is actually smooth. Mild solutions are obtained in
several spaces with the right homogeneity to allow the existence of
self-similar solutions.
After publication, the managing editors were informed that key
results in this manuscript were ''borrowed" from the article below,
without the proper citation.
The reader should be aware of this claim and decide on her/his
own about the originality of this article.
[1] Jose A. Carrillo, Lucas C. F. Ferreira;
Self-similar solutions and large time asymptotics for the dissipative
quasi-geostrophic equations, HYKE Preprints, 2005-10,
http://www.hyke.org/preprint/index.php
Submitted April 24, 2005. Published June 15, 2005.
Math Subject Classifications: 35Q35, 35A07.
Key Words: Quasi-geostrophic equation; local spaces; mild solutions;
self-similar solutions
Show me the
PDF file (250K),
TEX file for this article.
Sadek Gala
Université d'Evry Val d'Essonne
Département de Mathématiques
Bd F. Mitterrand. 91025 Evry Cedex. France
email: Sadek.Gala@maths.univ-evry.fr |
Return to the EJDE web page
![$$\displaylines{
\partial_{t}\theta+u\nabla\theta+( -\Delta) ^{\gamma}\theta =0
\quad \hbox{on }\mathbb{R}^{d}\times] 0,+\infty[\cr
\theta( x,0) =\theta_{0}(x), \quad x\in\mathbb{R}^{d}
}$$](gifs/aa.gif)
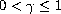 is a fixed parameter and the velocity field
is a fixed parameter and the velocity field
 is divergence free; i.e.,
is divergence free; i.e.,
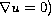 .
The initial data
.
The initial data
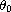 is taken in Banach
spaces of local measures (see text for the definition), such as Multipliers,
Lorentz and Morrey-Campanato spaces. We will focus on the subcritical case
is taken in Banach
spaces of local measures (see text for the definition), such as Multipliers,
Lorentz and Morrey-Campanato spaces. We will focus on the subcritical case
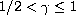 and we analyse the well-posedness of the
system in three basic spaces:
and we analyse the well-posedness of the
system in three basic spaces:
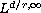 ,
,
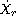 and
and
 ,
when the
solution is global for sufficiently small initial data. Furtheremore, we
prove that the solution is actually smooth. Mild solutions are obtained in
several spaces with the right homogeneity to allow the existence of
self-similar solutions.
,
when the
solution is global for sufficiently small initial data. Furtheremore, we
prove that the solution is actually smooth. Mild solutions are obtained in
several spaces with the right homogeneity to allow the existence of
self-similar solutions.