In this paper, we study the solutions to the Cauchy problem
![$$\displaylines{
(u_{tt}-\Delta u)_{g_s}+m^2u=f(u),\quad t\in (0, 1], x\in \mathbb{R}^3,\cr
u(1, x)=u_0\in {\dot B}^{\gamma}_{p, p}(\mathbb{R}^3),\quad
u_t(1, x)=u_1\in {\dot B}^{\gamma-1}_{p, p}(\mathbb{R}^3),
}$$](gifs/aa.gif)
where
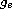 is the Reissner-Nordstrom metric;
is the Reissner-Nordstrom metric;
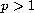 ,
,
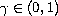 ,
,
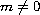 are constants,
are constants,
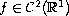 ,
,
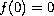 ,
,
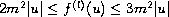 ,
,
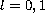 .
More precisely we prove that
the Cauchy problem has unique nontrivial solution in
.
More precisely we prove that
the Cauchy problem has unique nontrivial solution in
![$\mathcal{C}((0, 1]{\dot B}^{\gamma}_{p, p}(\mathbb{R}^+))$](gifs/aj.gif) ,
,
![$$
u(t,r)= \cases
v(t)\omega(r)&\hbox{for }t\in (0, 1],\; r\leq r_1\\
0&\hbox{for } t\in (0, 1],\; r\geq r_1,
\endcases
$$](gifs/ak.gif)
where
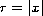 ,
and
,
and
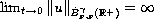 .
.
Svetlin G. Georgiev
Abstract:
In this paper, we study the solutions to the
Cauchy problem
![$$\displaylines{
(u_{tt}-\Delta u)_{g_s}+m^2u=f(u),\quad t\in (0, 1], x\in \mathbb{R}^3,\cr
u(1, x)=u_0\in {\dot B}^{\gamma}_{p, p}(\mathbb{R}^3),\quad
u_t(1, x)=u_1\in {\dot B}^{\gamma-1}_{p, p}(\mathbb{R}^3),
}$$](gifs/aa.gif)
where
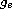 is the Reissner-Nordstrom metric;
is the Reissner-Nordstrom metric;
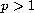 ,
,
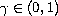 ,
,
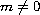 are constants,
are constants,
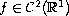 ,
,
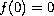 ,
,
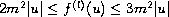 ,
,
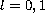 .
More precisely we prove that
the Cauchy problem has unique nontrivial solution in
.
More precisely we prove that
the Cauchy problem has unique nontrivial solution in
![$\mathcal{C}((0, 1]{\dot B}^{\gamma}_{p, p}(\mathbb{R}^+))$](gifs/aj.gif) ,
,
![$$
u(t,r)= \cases
v(t)\omega(r)&\hbox{for }t\in (0, 1],\; r\leq r_1\\
0&\hbox{for } t\in (0, 1],\; r\geq r_1,
\endcases
$$](gifs/ak.gif)
where
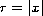 ,
and
,
and
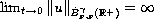 .
.
Submitted March 14, 2005. Published June 27, 2005.
Math Subject Classifications: 35L05, 35L15.
Key Words: Partial differential equation; Klein-Gordon; blow up.
Show me the PDF file (288K), TEX file for this article.
 |
Svetlin Georgiev Georgiev University of Sofia Faculty of Mathematics and Informatics Department of Differential Equations, Bulgaria email: sgg2000bg@yahoo.com |
|---|
Return to the EJDE web page