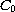 -semigroups
-semigroups
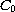 -semigroups
-semigroups
Eero Immonen
Abstract:
We show that the existence of a nontrivial bounded uniformly
continuous (BUC) complete trajectory for a
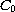 -semigroup
-semigroup
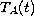 generated by an operator
generated by an operator
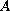 in a Banach space
in a Banach space
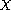 is equivalent
to the existence of a solution
is equivalent
to the existence of a solution
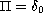 to the homogenous
operator equation
to the homogenous
operator equation
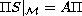 . Here
. Here
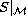 generates the shift
generates the shift
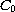 -group
-group
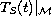 in a closed
translation-invariant subspace
in a closed
translation-invariant subspace
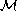 of
of
 ,
and
,
and
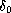 is the point evaluation at the origin. If, in addition,
is the point evaluation at the origin. If, in addition,
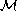 is operator-invariant and
is operator-invariant and
 is any solution of
is any solution of
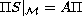 , then all functions
, then all functions
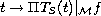 ,
,
 ,
are complete trajectories for
,
are complete trajectories for
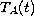 in
in
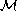 .
We connect these results
to the study of regular admissibility of Banach function spaces for
.
We connect these results
to the study of regular admissibility of Banach function spaces for
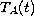 ;
among the new results are perturbation theorems for regular
admissibility and complete trajectories.
Finally, we show how strong stability of a
;
among the new results are perturbation theorems for regular
admissibility and complete trajectories.
Finally, we show how strong stability of a
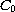 -semigroup
can be
characterized by the nonexistence of nontrivial bounded complete
trajectories for the sun-dual semigroup, and by the surjective solvability
of an operator equation
-semigroup
can be
characterized by the nonexistence of nontrivial bounded complete
trajectories for the sun-dual semigroup, and by the surjective solvability
of an operator equation
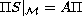 .
.
Submitted April 17, 2005. Published June 30, 2005.
Math Subject Classifications: 47D03.
Key Words: Sylvester operator equation; regularly admissible space;
complete nontrivial trajectory;
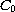 -semigroup; exponential stability;
strong stability; exponential dichotomy.
-semigroup; exponential stability;
strong stability; exponential dichotomy.
Show me the PDF file (282K), TEX file for this article.
| Eero Immonen Institute of Mathematics Tampere University of Technology PL 553, 33101 Tampere, Finland email: Eero.Immonen@tut.fi |
Return to the EJDE web page