Electron. J. Diff. Eqns., Vol. 2005(2005), No. 86, pp. 1-9.
Positive solutions and eigenvalues of nonlocal
boundary-value problems
Jifeng Chu, Zhongcheng Zhou
Abstract:
We study the ordinary differential equation
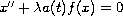 with the boundary conditions
with the boundary conditions
 and
and
 .
We characterize values of
.
We characterize values of
 for which boundary-value
problem has a positive solution. Also we find appropriate
intervals for
for which boundary-value
problem has a positive solution. Also we find appropriate
intervals for
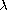 so that there are two positive solutions.
so that there are two positive solutions.
Submitted April 18, 2005. Published July 27, 2005.
Math Subject Classifications: 34B15
Key Words: Nonlocal boundary-value problems;
Positive solutions; eigenvalues;
fixed point theorem in cones.
Show me the
PDF file (215K),
TEX file, and other files for this article.
 |
Jifeng Chu
Department of Applied Mathematics
College of Sciences, Hohai University
Nanjing 210098, China
email: jifengchu@hhu.edu.cn |
|---|
 |
Zhongcheng Zhou
School of Mathematics and Finance
Southwest Normal University
Chongqing 400715, China
email: zhouzc@swnu.edu.cn
|
|---|
Return to the EJDE web page
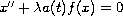 with the boundary conditions
with the boundary conditions
 and
and
 .
We characterize values of
.
We characterize values of
 for which boundary-value
problem has a positive solution. Also we find appropriate
intervals for
for which boundary-value
problem has a positive solution. Also we find appropriate
intervals for
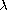 so that there are two positive solutions.
so that there are two positive solutions.

