Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 09, pp. 1-6.
Nonexistence of solutions to KPP-type equations
of dimension greater than or equal to one
Janos Englander, Peter L. Simon
Abstract:
In this article, we consider a semilinear elliptic equations of
the form
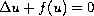 ,
where
,
where
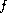 is a concave function. We
prove for arbitrary dimensions that there is no solution bounded
in
is a concave function. We
prove for arbitrary dimensions that there is no solution bounded
in
 .
The significance of this result in probability theory
is also discussed.
.
The significance of this result in probability theory
is also discussed.
Submitted September 19, 2005. Published January 24, 2006.
Math Subject Classifications: 35J60, 35J65, 60J80.
Key Words: KPP-equation; semilinear elliptic equations;
positive bounded solutions; branching Brownian-motion.
Show me the
PDF file (201K),
TEX file for this article.
 |
János Engländer
Department of Statistics and Applied Probability
University of California
Santa Barbara, CA 93106-3110, USA
email: englander@pstat.ucsb.edu
http://www.pstat.ucsb.edu/faculty/englander |
|---|
 |
Péter L. Simon
Department of Applied Analysis, Eötvös Loránd University
Pázmány Péter Sétány 1/C, H-1117 Budapest,
Hungary
email: simonp@cs.elte.hu
http://www.cs.elte.hu/~simonp
|
|---|
Return to the EJDE web page
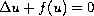 ,
where
,
where
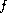 is a concave function. We
prove for arbitrary dimensions that there is no solution bounded
in
is a concave function. We
prove for arbitrary dimensions that there is no solution bounded
in
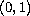 .
The significance of this result in probability theory
is also discussed.
.
The significance of this result in probability theory
is also discussed.

