Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 111, pp. 1-9.
On the first eigenvalue of the Steklov eigenvalue problem for the
infinity Laplacian
An Le
Abstract:
Let
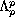 be the best Sobolev embedding constant of
be the best Sobolev embedding constant of
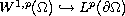 ,
where
,
where
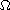 is a smooth bounded domain in
is a smooth bounded domain in
 .
We prove that as
.
We prove that as
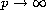 the sequence
the sequence
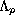 converges to a constant independent of the shape
and the volume of
converges to a constant independent of the shape
and the volume of
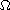 ,
namely 1.
Moreover, for any sequence of eigenfunctions
,
namely 1.
Moreover, for any sequence of eigenfunctions
 (associated with
(associated with
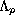 ),
normalized by
),
normalized by
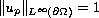 ,
there is a subsequence converging to a limit function
,
there is a subsequence converging to a limit function
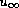 which satisfies, in the viscosity sense, an
which satisfies, in the viscosity sense, an
 -Laplacian
equation with a boundary condition.
-Laplacian
equation with a boundary condition.
Submitted August 4, 2006. Published September 18, 2006.
Math Subject Classifications: 35J50, 35J55, 35J60, 35J65, 35P30.
Key Words: Nonlinear elliptic equations; eigenvalue problems;
p-Laplacian; nonlinear boundary condition;
Steklov problem; viscosity solutions.
Show me the
PDF file (220K),
TEX file for this article.
 |
An Lê
Department of Mathematics and Statistics
Utah State University
Logan, Utah 84322, USA
email: anle@cc.usu.edu |
|---|
Return to the EJDE web page
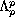 be the best Sobolev embedding constant of
be the best Sobolev embedding constant of
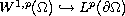 ,
where
,
where
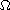 is a smooth bounded domain in
is a smooth bounded domain in
 .
We prove that as
.
We prove that as
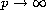 the sequence
the sequence
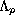 converges to a constant independent of the shape
and the volume of
converges to a constant independent of the shape
and the volume of
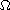 ,
namely 1.
Moreover, for any sequence of eigenfunctions
,
namely 1.
Moreover, for any sequence of eigenfunctions
 (associated with
(associated with
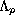 ),
normalized by
),
normalized by
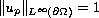 ,
there is a subsequence converging to a limit function
,
there is a subsequence converging to a limit function
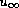 which satisfies, in the viscosity sense, an
which satisfies, in the viscosity sense, an
 -Laplacian
equation with a boundary condition.
-Laplacian
equation with a boundary condition.
