Generalized eigenfunctions of the 3-dimensional relativistic Schrodinger operator
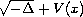 with
with
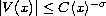 ,
,
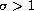 ,
are considered. We construct the generalized eigenfunctions
by exploiting results on the limiting absorption principle.
We compute explicitly the integral kernel of
,
are considered. We construct the generalized eigenfunctions
by exploiting results on the limiting absorption principle.
We compute explicitly the integral kernel of
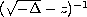 ,
,
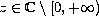 ,
which has nothing in common with
the integral kernel of
,
which has nothing in common with
the integral kernel of
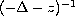 ,
but the leading term of the integral kernels of the boundary
values
,
but the leading term of the integral kernels of the boundary
values
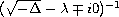 ,
,
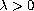 ,
turn out to be the same, up to a constant, as the integral
kernels of the boundary values
,
turn out to be the same, up to a constant, as the integral
kernels of the boundary values
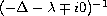 .
This fact enables us to show that
the asymptotic behavior, as
.
This fact enables us to show that
the asymptotic behavior, as
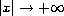 , of
the generalized eigenfunction of
, of
the generalized eigenfunction of
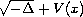 is equal to
the sum of a plane wave and a spherical wave when
is equal to
the sum of a plane wave and a spherical wave when
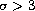 .
.
