Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 137, pp. 1-11.
A property of the H-convergence for elasticity in perforated domains
Hamid Haddadou
Abstract:
In this article, we obtain the
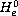 -convergence
as a limit case of the
-convergence
as a limit case of the
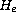 -convergence.
More precisely, if
-convergence.
More precisely, if
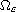 is a perforated domain with (admissible)
holes
is a perforated domain with (admissible)
holes
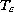 and
and
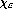 denote its characteristic function and if
denote its characteristic function and if
 ,
we show how the behavior as
,
we show how the behavior as
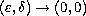 of the double sequence of tensors
of the double sequence of tensors
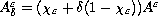 is connected to
is connected to
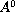 .
These results extend
those given by Cioranescu, Damlamian, Donato and
Mascarenhas in [3] for the
.
These results extend
those given by Cioranescu, Damlamian, Donato and
Mascarenhas in [3] for the
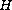 -convergence
of the scalar
second elliptic operators to the linearized elasticity systems.
-convergence
of the scalar
second elliptic operators to the linearized elasticity systems.
Submitted July 6, 2006. Published October 31, 2006.
Math Subject Classifications: 35B40, 74B05.
Key Words: Homogenization; H-convergence; linearized elasticity system;
perforated domains.
Show me the
PDF file (250K),
TEX file for this article.
 |
Hamid Haddadou
Institut Nationale de formation en Informatique
BP 68, Oued Smar, El Harrach
Alger, Algérie
email: h_haddadou@ini.dz |
|---|
Return to the EJDE web page
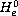 -convergence
as a limit case of the
-convergence
as a limit case of the
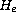 -convergence.
More precisely, if
-convergence.
More precisely, if
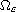 is a perforated domain with (admissible)
holes
is a perforated domain with (admissible)
holes
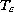 and
and
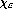 denote its characteristic function and if
denote its characteristic function and if
 ,
we show how the behavior as
,
we show how the behavior as
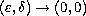 of the double sequence of tensors
of the double sequence of tensors
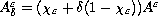 is connected to
is connected to
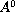 .
These results extend
those given by Cioranescu, Damlamian, Donato and
Mascarenhas in [3] for the
.
These results extend
those given by Cioranescu, Damlamian, Donato and
Mascarenhas in [3] for the
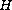 -convergence
of the scalar
second elliptic operators to the linearized elasticity systems.
-convergence
of the scalar
second elliptic operators to the linearized elasticity systems.
