Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 142, pp. 1-15.
Exact controllability of generalized Hammerstein type integral
equation and applications
Dimplekumar N. Chalishajar, Raju K. George
Abstract:
In this article, we study the exact controllability of an abstract
model described by the controlled generalized Hammerstein type
integral equation
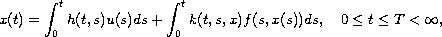
where, the state
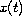 lies in a Hilbert space
lies in a Hilbert space
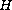 and
control
and
control
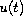 lies another Hilbert space
lies another Hilbert space
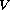 for each time
for each time
![$t \in I=[0,T]$](gifs/af.gif) ,
,
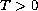 .
We establish the controllability
result under suitable assumptions on
.
We establish the controllability
result under suitable assumptions on
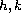 and
and
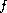 using the monotone operator theory.
using the monotone operator theory.
Submitted April 23, 2006. Published November 9, 2006.
Math Subject Classifications: 93B05, 93C10.
Key Words: Exact controllability; Hammerstein type
integral equation; monotone operator; solution operator.
Show me the
PDF file (276K),
TEX file for this article.
 |
Dimplekumar N. Chalishajar
Department of Applied Mathematics
Sardar Vallabhbhai Patel Institute of Technology (SVIT)
Gujarat University, Vasad-388306. Gujarat State, India
email: dipu17370@yahoo.com, dimple.chalishajar@gmail.com
|
|---|
 |
Raju K. George
Department of Mathematical Sciences
University of Delaware, Newark, DE 19716, USA
email: rkgeorgemsu@yahoo.com |
|---|
Return to the EJDE web page
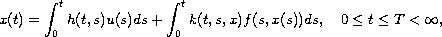
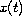 lies in a Hilbert space
lies in a Hilbert space
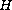 and
control
and
control
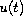 lies another Hilbert space
lies another Hilbert space
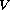 for each time
for each time
![$t \in I=[0,T]$](gifs/af.gif) ,
,
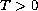 .
We establish the controllability
result under suitable assumptions on
.
We establish the controllability
result under suitable assumptions on
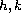 and
and
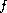 using the monotone operator theory.
using the monotone operator theory.

