Electron. J. Diff. Eqns., Vol. 2006(2006), No. 39, pp. 1-10.

Positive solutions of singular fourth-order boundary-value problems

Yujun Cui, Yumei Zou

Abstract:
In this paper, we present necessary and sufficient conditions for the existence of positive $C^3[0,1]\cap C^4(0,1)$ solutions for the singular boundary-value problem
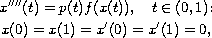
$$\displaylines{ x''''(t)=p(t)f(x(t)),\quad t\in(0,1);\cr x(0)=x(1)=x'(0)=x'(1)=0, }$$
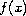where $f(x)$ is either superlinear or sublinear, 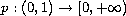$p:(0,1)\to [0,+\infty)$ may be singular at both ends 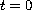$t=0$ and $t=1$. For this goal, we use fixed-point index results.

Submitted September 6, 2005. Published March 21, 2006
Math Subject Classifications: 34A34, 34B15, 45G15.
Key Words: Singular boundary value problem; fixed point theorem; positive solution.

Show me the PDF file (213K), TEX file for this article.

Yujun Cui
Department of Applied Mathematics
Shandong University of Science and technology
Qingdao, 266510, China
email: cyj720201@163.com
  Yumei Zou
Department of Applied Mathematics
Shandong University of Science and technology
Qingdao, 266510, China

Return to the EJDE web page