Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 62, pp. 1-19.
Boundary and initial value problems for second-order
neutral functional differential equations
Hoan Hoa Le, Thi Phuong Ngoc Le
Abstract:
In this paper, we consider the three-point boundary-value problem
for the second order neutral functional differential equation
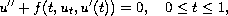
with the three-point boundary condition
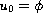 ,
,
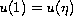 .
Under suitable
assumptions on the function
.
Under suitable
assumptions on the function
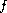 we prove the existence,
uniqueness and continuous dependence of solutions.
As an application of the methods used, we study the existence
of solutions for the same equation with a "mixed" boundary
condition
we prove the existence,
uniqueness and continuous dependence of solutions.
As an application of the methods used, we study the existence
of solutions for the same equation with a "mixed" boundary
condition
![$u_0 = \phi, u(1) = \alpha [u'(\eta) - u'(0)]$](gifs/ae.gif) ,
or with an initial condition
,
or with an initial condition
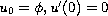 .
For the initial-value problem, the uniqueness and
continuous dependence of solutions are also considered.
Furthermore, the paper shows that the solution
set of the initial-value problem is nonempty, compact and
connected. Our approach is based on the fixed point theory.
.
For the initial-value problem, the uniqueness and
continuous dependence of solutions are also considered.
Furthermore, the paper shows that the solution
set of the initial-value problem is nonempty, compact and
connected. Our approach is based on the fixed point theory.
Submitted February 20, 2006. Published May 11, 2006.
Math Subject Classifications: 34M50, 34K40.
Key Words: Three-point boundary-value problem; topological degree;
Leray-Schauder nonlinear alternative; Contraction mapping principle.
Show me the
PDF file (295K),
TEX file for this article.
 |
Hoan Hoa Le
Department of Mathematics
Ho Chi Minh City University of Education
280 An Duong Vuong Str., Dist. 5, Ho Chi Minh City, Vietnam
|
|---|
 |
Thi Phuong Ngoc Le
Nha Trang Educational College
01 Nguyen Chanh Str., Nha Trang City, Vietnam
email: phuongngoccdsp@dng.vnn.vn lephuongngoc@netcenter-vn.net
|
|---|
Return to the EJDE web page
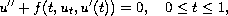
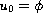 ,
,
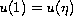 .
Under suitable
assumptions on the function
.
Under suitable
assumptions on the function
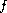 we prove the existence,
uniqueness and continuous dependence of solutions.
As an application of the methods used, we study the existence
of solutions for the same equation with a "mixed" boundary
condition
we prove the existence,
uniqueness and continuous dependence of solutions.
As an application of the methods used, we study the existence
of solutions for the same equation with a "mixed" boundary
condition
![$u_0 = \phi, u(1) = \alpha [u'(\eta) - u'(0)]$](gifs/ae.gif) ,
or with an initial condition
,
or with an initial condition
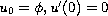 .
For the initial-value problem, the uniqueness and
continuous dependence of solutions are also considered.
Furthermore, the paper shows that the solution
set of the initial-value problem is nonempty, compact and
connected. Our approach is based on the fixed point theory.
.
For the initial-value problem, the uniqueness and
continuous dependence of solutions are also considered.
Furthermore, the paper shows that the solution
set of the initial-value problem is nonempty, compact and
connected. Our approach is based on the fixed point theory.

